Quando si parla di nomi come questo, ogni presentazione risulta superflua; tuttavia non posso fare a meno di spendere alcune brevi parole su Albino Carbognani, che oltre ad essere uno dei grandi nomi dell’astronomia nel nostro paese, e un amico di vecchia data, si rivela essere persona sempre capace di sorprendere. Uno di quelli che riesce a mostrarti, a farti capire davvero, che chi nasce astrofilo, astrofilo rimane. Per tutta la vita! Al di là dei successi conseguiti nel mondo scientifico; al di là della ricerca professionale; al di là persino degli strumenti pazzeschi coi quali puoi operare ogni santo giorno, fino a renderli routine.
L’astrofilia, ci insegna Albino, è qualcosa in più, qualcosa che va oltre la semplice osservazione amatoriale del cielo.
L’astrofilia è contemplazione, l’astrofilia è stupore, l’astrofilia è passione; grande, che non si spegne mai. È quella strana forma di sana follia che ti fa svegliare nel cuore della notte, anche se qualcuno all’altro capo del letto ti invita a restare; anche se fuori c’è un mondo assonnato, avvolto dal gelo. Ti fa alzare, preparare, impegnare e faticare per ore, se serve, al solo scopo di poter osservare ancora una volta quel piccolo puntino luminoso lassù… È quell’istinto che ti spinge a fare e impegnarti ancora, con il cuore, con l’anima, con il poco tempo libero che hai, con i conti che non tornano mai, anche quando già in tanti, prima di te, si sono cimentati con quel CCD su quella galassia.
È un desiderio, una fame, che non passa mai; neanche quando sai, come il nostro Albino, che lo strumento che stai per usare, il TUO telescopio, l’estrinsecazione materiale di ciò che fa di te un astrofilo, all’osservatorio non farebbe nemmeno la funzione di guida.
Ecco, questo è il modo in cui voglio introdurre oggi lo splendido articolo di Albino, che pubblico qui sotto: un grande lavoro, di un grande amico, ma soprattutto di un grande astrofilo!
LUCA ZANCHETTA – TELESKOP SERVICE ITALIA
Piccoli punti di luce che si muovono in cielo
Come e perché fare la fotometria degli asteroidi
Albino Carbognani, Ph.D.
Spesso e volentieri gli astrofili che usano telescopio, montatura computerizzata e camera CCD hanno come obiettivo principale l’astrofotografia di oggetti deep-sky, cioè la ripresa di nebulose, ammassi stellari e galassie, principalmente per fini estetici con la rincorsa al dettaglio più tenue. Si tratta di una attività che può dare molte soddisfazioni, i sottili disegni delle nebulose e le delicate trame delle galassie hanno il loro indubbio fascino. Peraltro l’astrofotografa richiede un notevole investimento in attrezzatura piuttosto sofisticata, senza contare il tempo che richiede per ottenere buoni risultati.
Considerato l’investimento sulla strumentazione può essere interessante chiedersi come si possa svolgere anche una attività interessante dal punto di vista scientifico: l’imaging deep-sky non esaurisce sicuramente tutte le possibilità di utilizzo. Certo, quando si fa scienza si devono compiere delle misure e questo può complicare la strada da percorrere per ottenere dei risultati, ma la soddisfazione alla fine sarà veramente notevole. Sotto questo punto di vista gli asteroidi offrono diverse possibilità entusiasmanti!
L’astrometria dei NEA
La prima attività scientifica cui si può pensare quando si tratta di corpi minori è la caratterizzazione orbitale degli asteroidi near-Earth (NEA). Si tratta degli asteroidi che con la loro orbita possono passare a meno di 0,3 UA dalla Terra. Sulla scala dei milioni di anni le orbite dei NEA sono talmente instabili (cioè caotiche) che rappresentano un potenziale rischio impatto per il nostro pianeta. Complessivamente ne sono noti più di 15.600 e negli ultimi anni la media delle nuove scoperte è di circa 1000 ogni anno. Grosso modo è noto il 95% dei NEA con diametro pari o superiore al km, poco meno di 1000 oggetti. L’obiettivo ora è la scoperta e caratterizzazione della maggior parte degli oggetti con diametro superiore ai 140 m, attività che richiederà ancora parecchi anni per essere portata a termine perché più si scende con il diametro e maggiore è il numero degli oggetti. Il valore minimo di 140 m per il diametro può sembrare piccolo, in realtà non lo è affatto se si considera che la celebre Catastrofe di Tunguska del 30 giugno 1908 è stata provocata dalla caduta di un piccolo asteroide di soli 50 metri di diametro! In effetti il danno che un asteroide è in grado di provocare è sì proporzionale alla massa ma anche al quadrato della velocità di caduta. Essendo quest’ultima dell’ordine di svariate decine di km/s ecco che anche un piccolo oggetto può causare un danno rilevante.
Un tipico NEA è quindi un oggetto “piccolo” e anche molto scuro perché la superficie assorbe gran parte della luce solare. Per questo motivo un NEA può essere scoperto solo quando è già in prossimità della Terra e approssimativamente nella direzione opposta al Sole. A questo scopo è necessario impiegare grandi telescopi con ampi campi di vista, in grado di scansionare l’intera sfera celeste nel più breve tempo possibile e ripetere il processo in continuazione. Chiaramente attrezzature di questo tipo sono oltre le possibilità di un astrofilo. In effetti le survey che si occupano della scoperta dei NEA sono tutte statunitensi, fra quelle di maggior successo ci sono la Catalina Sky-Survey in Arizona, che utilizza due telescopi da 68 e 150cm di apertura, e Pan-STARSS nelle Hawaii con due telescopi da 180 cm di diametro.
Il contributo degli astrofili diventa importante nella fase successiva alla discovery, quando gli oggetti appena scoperti vengono inseriti nella NEO Confirmation Page (NEOCP) del Minor Planet Center per la conferma e la determinazione preliminare dell’orbita. Peraltro contribuire alla caratterizzazione astrometrica di un NEA, oltre al valore scientifico del lavoro, ha il suo indubbio fascino!
Purtroppo però, negli ultimi anni si è assistito ad un progressivo aumento della magnitudine dei NEA da confermare, come è logico aspettarsi visto che tutti gli asteroidi “grossi” oramai sono noti. Di conseguenza, mentre nel 2005 anche con un piccolo telescopio da 25-30 cm di diametro c’era solo l’imbarazzo della scelta perché gli oggetti avevano una magnitudine apparente attorno alla +18, ora si veleggia attorno alla +20 con tendenza a salire. Chiaramente se il diametro del telescopio è troppo piccolo, diventa difficile ottenere delle immagini misurabili per dare il proprio contributo.
Tuttavia la determinazione dell’orbita non esaurisce tutto quello che si può fare su un NEA o, meglio, su un asteroide di Fascia Principale (MBA). Infatti, una volta nota l’orbita, dell’asteroide in sé non conosciamo ancora niente. Per questo il passo successivo all’astrometria è la fotometria, che permette di studiare fisicamente l’asteroide: in primo luogo di determinare il periodo di rotazione. La buona notizia è che si tratta di un campo di ricerca dove anche con un piccolo telescopio si può dare il proprio contributo e che si possono fare delle scoperte del tutto inattese!
Attualmente, nel database del Minor Planet Center ci sono circa 474.000 asteroidi numerati, di cui appena 20.200 (circa il 4,3 %), hanno un nome. Dai dati presenti nell’Asteroid Lightcurve Database, uno dei punti di riferimento per chi si occupa di fotometria degli asteroidi, gli oggetti numerati di cui è noto il periodo di rotazione sono circa 16.000, pochissimi rispetto al totale dei numerati: solo il 3,4%. Considerate le magnitudini in ballo per un tipico MBA (da +14 alla +16), si tratta di un settore dove si può dare il proprio contributo originale anche con telescopi di piccolo diametro (20-30 cm). La caratterizzazione fisica degli asteroidi è un campo di ricerca con ampie possibilità di sviluppo, anche per i prossimi anni, e poi fare la fotometria degli asteroidi permette di caratterizzare fisicamente questi antichi testimoni dell’evoluzione del Sistema Solare.
La strumentazione per la fotometria
Vediamo qualche indicazione strumentale sul “setup ideale” da utilizzare per la fotometria degli asteroidi. Prima di tutto il telescopio deve avere almeno 20 cm di diametro e deve essere accessoriato con una buona camera CCD a 16 bit, cioè con circa 216 = 65.536 livelli di intensità possibili. La camera deve essere almeno raffreddata con una cella Peltier avente un delta T di 30-40 °C rispetto alla temperatura ambiente e deve essere del tipo non-ABG, cioè senza antiblooming. L’antiblooming, utile per l’estetica delle foto deep-sky, non deve essere presente perché con quest’ultimo si perde in sensibilità, risoluzione e risposta lineare tutte caratteristiche importanti quando si fa ricerca scientifica. Il sensore deve essere del tipo in bianco/nero per massimizzare l’efficienza quantica e la camera può essere dotata di una ruota portafiltri con filtri standard B, V, R e I di Johnson-Cousins. La scala dell’immagine CCD può oscillare da 1 a 2 secondi d’arco per pixel, dipende dalle condizioni di seeing locali, in modo tale che il diametro stellare sia descritto da almeno 2-3 pixel. In ogni caso, per questo tipo di lavoro non sono necessarie le lunghe focali tipiche delle riprese planetarie in alta risoluzione, o i lunghissimi tempi di posa caratteristici della fotografia deep-sky.
Per avere misure fotometriche attendibili è necessario che l’immagine dell’asteroide non sia in saturazione ed è obbligatorio fare i file di calibrazione standard da applicare alle immagini, riprese ovviamente nel formato FITS (Flexible Image Transport System) standard. Da evitare nel modo più assoluto formati compressi come il jpg perché si perde l’informazione fotometrica. I file di calibrazione necessari sono il master dark, ottenuto dalla mediana di alcune decine di dark frame presi alla stessa temperatura e identico tempo di esposizione delle immagini e il master flat, ottenuto dalla media di almeno alcune decine di flat frame singoli, ovviamente ciascuno corretto con il proprio master dark.
La presenza di un telescopio di guida e di una camera di autoguida con porta ST4 da collegare alla montatura può non essere necessaria se la montatura equatoriale è sufficientemente stabile e robusta, visto che i tempi di posa tipici sono al più di alcuni minuti. La montatura equatoriale deve essere preferibilmente del tipo a forcella per evitare i problemi fotometrici che può dare il meridian flip, l’inversione degli assi che avviene attorno al passaggio in meridiano e che, di solito, affligge le equatoriali alla tedesca. Per compensare il meridian flip si può ritardare il più a lungo possibile l’inversione della montatura in questo modo si possono ottenere curve di luce più continue, cioè senza “gradini”. Caldamente consigliata infine la presenza del computer per il puntamento automatico, per non perdere tempo prezioso nella fase di ricerca degli asteroidi in cielo.
Per quanto riguarda la scelta dei target interessanti, NEA o MBA, si possono consultare le ultime pagine del Minor Planet Bulletin (vedi http://www.minorplanet.info/mpbdownloads.html), la rivista scientifica internazionale liberamente disponibile in pdf e punto di riferimento per professionisti e non per quanto riguarda la fotometria degli asteroidi.
La fotometria d’apertura
In astrofisica con il generico termine fotometria si indica lo studio della radiazione ottica emessa da un corpo celeste, avente una lunghezza d’onda fra 400 e 700 nm (1 nm = 10-9 m). Si parla invece di radiometria quando si considera anche la radiazione emessa al di fuori dell’intervallo del visibile.
In una tipica immagine con una posa superiore alla decina di secondi, le sorgenti puntiformi (stelle, asteroidi ecc.), vengono convolute dagli effetti della turbolenza atmosferica, dall’ottica del telescopio, dalle vibrazioni del tubo ottico e così via. Il risultato è che la distribuzione della luce sul sensore può essere descritta da una superficie gaussiana. Di solito la fotometria che viene fatta sulle immagini CCD, dopo la correzione per master dark e master flat, è la fotometria d’apertura. Con questa tecnica si sovrappone al target un anulus di misura con un diametro pari a 3 volte la full width at half maximum (FWHM), cioè la larghezza a mezza altezza del tipico profilo gaussiano che ha la sorgente puntiforme. Prendere 3 volte la FWHM di una sorgente puntiforme equivale a prendere un anello con un diametro pari a circa 7,1 volte il valore di sigma della gaussiana (vale la relazione 1 FWHM 2,355), quindi con 3 FWHM si è sicuri di includere praticamente tutto il segnale proveniente dalla sorgente puntiforme e raccolto dai pixel del CCD.

Figura 1. Gli anulus di misura di una sessione di fotometria d’apertura riguardante l’asteroide near-Earth 2002 WP. I cerchi gialli sono per il target, il verde è per la prima stella di confronto, i cerchi rossi sono per le altre quattro stelle di confronto.
Il CCD è un dispositivo a risposta lineare quindi l’intensità I di una stella (in unità arbitrarie), ottenuta sommando l’intensità di tutti i pixel che compongono l’immagine della stella (o dell’asteroide), all’interno dell’anello di misura sarà direttamente proporzionale al flusso luminoso ricevuto. All’intensità I del target va però tolto il valore del segnale proveniente dal fondo cielo e non dalla sorgente che ci interessa. Il valore della intensità del fondo cielo si ottiene leggendo il valore di intensità dei pixel posti in un anello più esterno ma concentrico a quello di misura della sorgente, possibilmente senza stelle di fondo (vedi Fig. 1). Se indichiamo con B il valore del fondo cielo (che si ottiene dal valore medio del pixel del fondo moltiplicato per il numero di pixel misurati del target), il segnale del solo target sarà dato da:
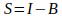 (1)
(1)
Noto il segnale S della sorgente, si può calcolare quella che è nota come magnitudine strumentale:
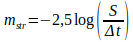 (2)
(2)
Qui t è il tempo di posa dell’immagine e S/t è una quantità proporzionale al flusso della sorgente. In questo modo si possono confrontare le magnitudini strumentali dello stesso target ma riprese con tempi di posa diversi.
Una volta misurata la magnitudine strumentale del target e delle stelle di confronto si può ottenere la variazione di magnitudine del target in funzione del tempo usando la tecnica della fotometria differenziale. La fotometria differenziale consiste essenzialmente nel misurare la differenza di magnitudine strumentale fra il target e la media delle magnitudini strumentali di due o più stelle di confronto scelte nello stesso campo di vista. Rispetto alla fotometria calibrata quella differenziale non richiede particolari condizioni di trasparenza costante del cielo e fornisce una buona accuratezza quando si tratta di misurare piccole variazioni di luminosità (inferiori al decimo di magnitudine), perché sia la luce del target sia delle stelle di confronto attraversano la stessa air-mass e, se hanno colore simile, subiscono anche gli stessi effetti di estinzione atmosferica.
In effetti, volendo essere pignoli, la differenza delle magnitudini strumentali differisce di una quantità proporzionale alla differenza degli indici di colore CI dalla differenza delle magnitudini apparenti vere secondo l’equazione:
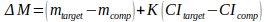 (3)
(3)
Tuttavia, nel caso degli asteroidi che riflettono la luce del Sole gli indici di colore sono grossomodo simili a quelli della nostra stella (B-V = 0,66 e V-R = 0,53), e se anche si osserva senza filtri ma si usano come stelle di confronto quelle di tipo solare, allora le differenze delle magnitudini strumentali saranno praticamente uguali alle differenze delle magnitudini apparenti perché il secondo termine della Eq. (3) si annulla o è molto piccolo.
Ovviamente, visto che gli asteroidi si spostano in cielo sia per effetto del moto orbitale attorno al Sole sia per effetto del moto eliocentrico della Terra, il set di stelle di confronto utilizzabile per la fotometria differenziale cambia da una sera all’altra (o da un’ora all’altra nel caso di NEA veloci), e una delle prime difficoltà da superare sarà il “raccordo” fra le curve di luce appartenenti a sessioni diverse, specialmente se il periodo di rotazione è molto lungo. Il problema del raccordo delle sessioni è evidente nel caso della semplice fotometria differenziale, mentre si riduce notevolmente con la fotometria assoluta, calibrata usando come riferimento fotometrico le stelle di confronto del campo di vista. Non entreremo nel dettaglio della fotometria calibrata, ma i cataloghi stellari utilizzabili, entro alcuni centesimi di magnitudine e per target fino alla mag +15, come riferimento per le magnitudini sono l’UCAC4 (USNO CCD Astrograph Catalog), il CMC15 (Carlsberg Meridian Catalogue) e l’ultima release dell’APASS (AAVSO Photometric All-Sky Survey).
La selezione dell’asteroide da osservare avviene in base agli obiettivi che ci si propone di raggiungere, alla magnitudine apparente, alla velocità angolare, al range di air-mass e al numero di ore che un asteroide può essere osservato (in generale più sono e meglio è). Anche in condizioni di bassa turbolenza atmosferica, il target deve essere ad almeno 25° di altezza sull’orizzonte (air-mass = 2,4), in modo da minimizzare gli effetti deleteri del cattivo seeing e dell’assorbimento atmosferico che abbassano il rapporto segnale/rumore.
Gli asteroidi si spostano sulla sfera celeste, non sono target statici specialmente i near-Earth, di conseguenza il tempo di esposizione è determinato in base alla necessità di avere una immagine del target relativamente puntiforme sull’immagine, anche se in campo fotometrico una certa elongazione è ben tollerata dai software di misura. Un tempo di esposizione ragionevole (in minuti) sarà dato dalla FWHM (in secondi d’arco) diviso per la velocità angolare del target (secondi d’arco/minuto). In questo modo si raddoppiano le dimensioni della FWHM nella direzione del moto dell’asteroide, una elongazione ancora facilmente misurabile. Le esposizioni tipiche sono di 30-240 s per i MBA, la cui velocità angolare tipica è di 0,5 arcsec/minuto, e di 5-120 s per i NEA con velocità tipiche di 5-10 arcsec/minuto.
Fissato il tempo di esposizione bisogna verificare su immagini di prova che il valore del rapporto segnale/rumore (o SNR, Signal to Noise Ratio), sia adeguato alla incertezza fotometrica che si vuole raggiungere. Questo è un punto importante, spesso sottovalutato: non basta che l’asteroide sia genericamente visibile sull’immagine per avere automaticamente una buona fotometria. Facendo qualche stima si trova che per avere una precisione fotometrica con una incertezza di 0,02 mag è necessario avere SNR ≈ 50. Un valore eccellente è SNR ≈ 100, perché l’incertezza scende a 0,01 mag mentre un valore ancora accettabile, specialmente per asteroidi con una discreta ampiezza della curva di luce, è SNR ≈ 25 a cui corrisponde una incertezza di circa 0,04 mag. Di solito il SNR viene stimato direttamente dal software fotometrico quindi non è necessario avventurarsi in calcoli complessi.
Uno dei software di riferimento per la fotometria degli asteroidi, sia differenziale sia calibrata, è MPO Canopus (http://www.minorplanetobserver.com/MPOSoftware/MPOCanopus.htm) di Brian Warner. Per la verità con Canopus è possibile anche la fotometria delle stelle variabili anche se non è il suo utilizzo principale. Questo programma richiede un certo periodo per l’apprendimento del corretto utilizzo, fase che non va saltata pena il rischio di ottenere risultati fotometrici errati o poco attendibili. Caldamente consigliata anche la lettura del libro “A Practical Guide to Lightcurve Photometry and Analysis”, scritto dallo stesso Warner ed edito dalla Springer, in cui vengono illustrati in dettaglio i principi della fotometria asteroidale. Sono diversi i settori dove la fotometria degli asteroidi può dare un contributo, fra questi vedremo in dettaglio:
-
La determinazione del periodo di rotazione
-
La spin-barrier e la “caccia” ai large super-fast rotator
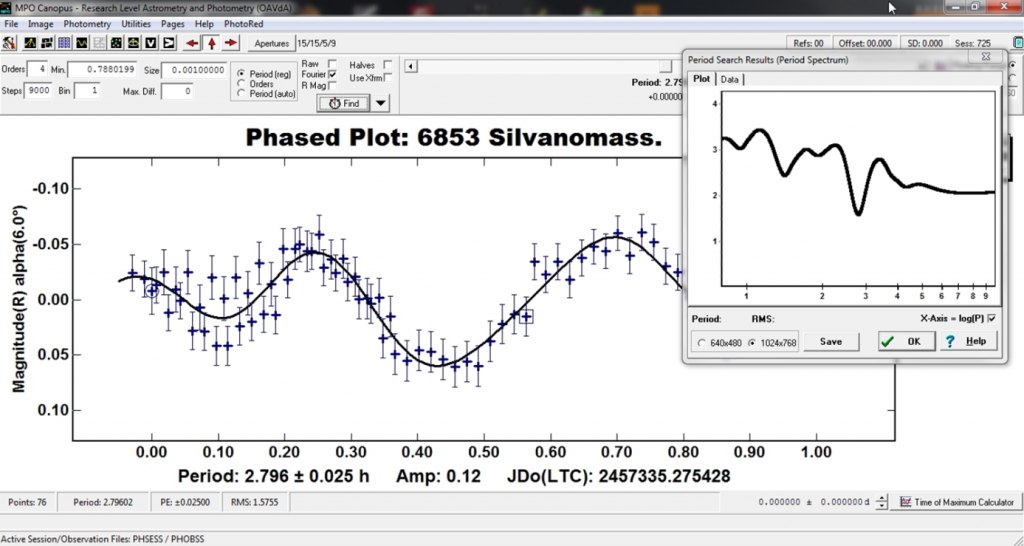
Figura 2. Una tipica sessione di MPO Canopus dopo l’analisi di Fourier, con la curva di luce dell’asteroide in fase e il corrispondente spettro dei periodi.
Determinazione del periodo di rotazione di un asteroide
Una tipica sessione di fotometria differenziale per la determinazione del periodo di rotazione di un asteroide vede la ripresa di immagini in modalità “fitta”, cioè una dietro l’altra, per una durata di diverse ore. Nel caso di asteroidi con periodo di rotazione completamente sconosciuto l’osservazione fotometrica deve essere fatta su almeno 2-3 notti consecutive prima di sperare di avere una buona misura (a meno che l’asteroide non sia un rotatore lento!). Generalmente, i periodi sono di 6-8 ore quindi almeno due-tre sessioni lunghe sono il minimo per avere una buona probabilità di successo. A questa segue la fase di riduzione dei dati: scelta delle stelle di confronto nel campo di vista, misura della magnitudine strumentale del target e delle confronto, calcolo della media delle magnitudini strumentali delle stelle di confronto da sottrarre al target e, infine, plot della magnitudine differenziale in funzione del tempo. Può capitare che una delle stelle scelta per il confronto non sia costante, in questo caso ci potrebbe scappare anche la scoperta di una nuova stella variabile. Per togliersi il dubbio è bene consultare il catalogo VSX, il Variable Star indeX, dell’AAVSO.
Da una o più sessioni della durata di alcune ore si otterrà la tipica curva di luce in fase di forma genericamente bimodale, cioè con due massimi e due minimi, come ci si aspetta da un generico corpo irregolare di forma allungata in rotazione attorno al proprio asse (Fig. 3). Ovviamente non sempre è così, ci possono essere curve trimodali o più complesse. In generale, vale la regola statistica che maggiore è l’ampiezza della curva di luce e più è probabile che la curva sia bimodale.
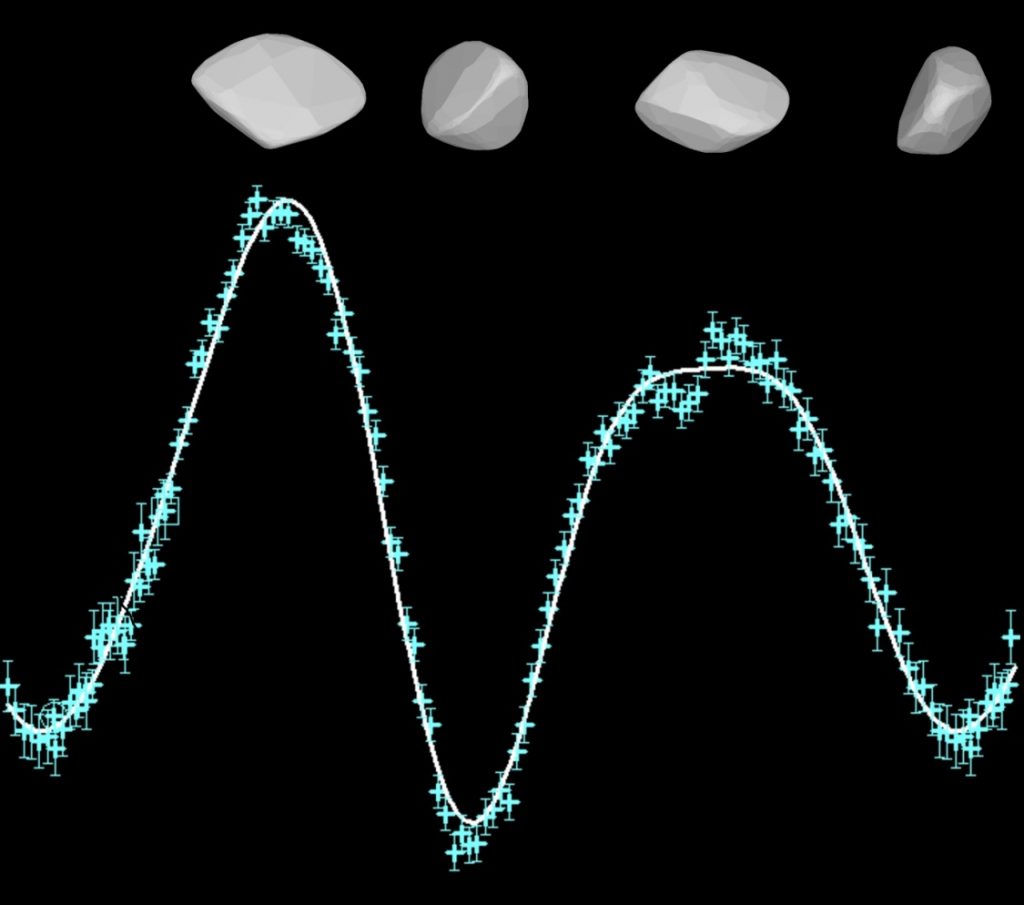
Figura 3. La curva di luce di un asteroide in rotazione attorno al proprio asse è una funzione periodica di periodo P e la forma più probabile è quella bimodale, cioè con due massimi e due minimi a seconda della superficie, più o meno estesa, illuminata dal Sole e rivolta verso la Terra. L’ampiezza della curva di luce si misura dal massimo al minimo assoluto.
Per la determinazione del periodo di rotazione degli asteroidi si usa l’analisi di Fourier. In MPO Canopus i dati fotometrici con le magnitudini ridotte di ogni sessione vengono fittate con una serie di Fourier di grado m finito a scelta. La stima del miglior periodo P che fitta tutti i dati è quello che fornisce il minore scarto fra la curva di Fourier teorica e i valori osservati della magnitudine (spettro dei periodi). Attenzione però: minimizzare lo scarto non garantisce l’unicità della soluzione per il periodo P, specie se la curva di luce è simmetrica, cioè massimi e minimi sono uguali fra loro o i dati non coprono una intera rotazione dell’asteroide! E ora vediamo perché può essere interessante determinare il periodo di rotazione di un asteroide.
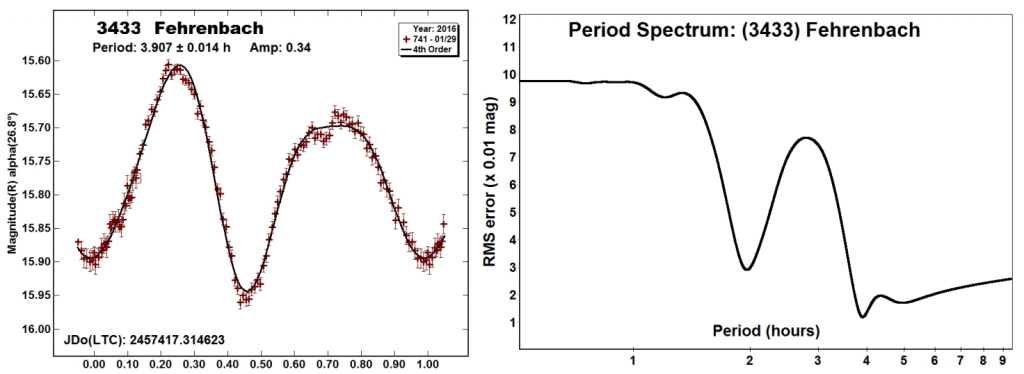
Figura 4. La curva di luce in fase, il fit di Fourier al 4° ordine e lo spettro dei periodi per l’asteroide di fascia principale 3433 Fehrenbach. L’ampiezza del curva di luce è abbastanza elevata e l’incertezza sui singoli punti è di circa 0,02 magnitudini. Lo spettro dei periodi mostra un minimo principale attorno alle 4 ore (soluzione bimodale) ed un minimo secondario attorno alle 2 ore (soluzione monomodale).
La cohesionless spin-barrier e gli asteroidi Large Super-Fast Rotator
Gli asteroidi sono corpi celesti soggetti ad interazione collisionale e la popolazione che vediamo oggi nella Fascia Principale (o main-belt), la zona di spazio compresa fra le orbite di Marte e Giove, è il risultato di miliardi di anni di evoluzione con gli asteroidi che si sono ripetutamente scontrati fra di loro. Questo ha portato alla distruzione parziale dei corpi maggiori, che sono in grado di resistere meglio alle collisioni, e alla distruzione parziale o totale dei corpi più piccoli. La scoperta delle famiglie di asteroidi fatta dall’astronomo giapponese Hirayama nel 1918 supporta questo quadro evolutivo.
L’analisi dei periodi di rotazione dei MBA e dei NEA che da essa derivano, mostra un comportamento che, a prima vista, non ci si aspetterebbe. Se si riporta su un grafico il periodo di rotazione di ciascun asteroide in funzione del diametro si scopre un comportamento affascinante: al di sopra di circa 150-200 metri di diametro i periodi di rotazione sono pari o superiori a circa 2,2 ore, mentre per i corpi più piccoli si possono avere valori anche di molto inferiori (Fig. 6).
Il valore limite di circa 2,2 ore è noto come “cohesionless spin-barrier”, cioè barriera rotazionale senza coesione. Per spiegare la presenza di questa “soglia di sbarramento” si ipotizza che gli asteroidi più piccoli di circa 150-200 m di diametro siano blocchi monolitici, le “schegge” createsi nella collisione di asteroidi con diametro maggiore, mentre i corpi più grandi sarebbero oggetti fratturati dalle collisioni e composti di blocchi più piccoli, non coesi fra di loro, ma tenuti semplicemente insieme dalla reciproca forza di gravità (struttura a “rubble-pile” senza coesione). Un notevole esempio di asteroide rubble-pile è il NEA (25143) Itokawa, esplorato nel 2005 dalla sonda giapponese Hayabusa (Fig. 5).

Figura 5. L’asteroide (25143) Itokawa ripreso dalla sonda giapponese Haybusa nel 2005. Itokawa è lungo circa 500 m e non presenta crateri da impatto sulla superficie, segno che si tratta di un aggregato di rocce e polveri risultato di una collisione catastrofica che ha smembrato l’asteroide progenitore (ISAS, JAXA).
Che le cose stiano così è dimostrato dal fatto che, se si calcola teoricamente il periodo limite di un asteroide sferico con una struttura a rubble-pile e una densità media di 2,2 g/cm3, si trova proprio un periodo limite di circa 2,2 ore. Per ottenere la formula che ci serve basta osservare che il periodo limite teorico per un asteroide rubble pile senza coesione (che chiameremo Plim), si trova imponendo che l’accelerazione superficiale dovuta alla rotazione dell’asteroide di raggio R e massa totale M sia pari a quella di gravità dell’asteroide stesso (condizione di moto circolare). In questo modo si impone la condizione che i blocchi superficiali di cui è fatto l’asteroide rubble-pile seguano un’orbita circolare con raggio pari a quello del corpo stesso. Per il periodo limite si trova:
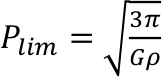 (4)
(4)
Nella Eq. (4) G è la costante di gravitazione universale e vale G = 6,674x10-11 m3 kg-1 s-2, mentre ρ è la densità media dell’asteroide. Si può verificare che per ρ = 2200 kg/m3 (equivalenti a 2,2 g/cm3), si ottiene un periodo limite di circa 2,2 ore. Se il periodo di rotazione diminuisce al di sotto di Plim, l’equilibrio si rompe e l’asteroide si separa nei blocchi distinti di cui è composto. Notare come questo risultato sia indipendente dal diametro stesso dell’asteroide: che sia grande o piccolo un asteroide rubble-pile che ruota troppo veloce si sfascia comunque! Secondo questo modello un asteroide rubble-pile che si trova con un periodo di rotazione al di sotto di quello della spin-barrier si frammenterà dando vita, ad esempio, ad un sistema binario. In effetti uno dei meccanismi più noti per la formazione degli asteroidi binari vede la fissione rotazionale di asteroidi rubble-pile che, a causa dell’effetto YORP, sono scesi con il periodo di rotazione al di sotto del valore della spin-barrier. Questo meccanismo spiega abbastanza bene le caratteristiche rotazionali dei primari fra le coppie di asteroidi, oggetti che hanno orbita eliocentrica simile ma che non sono legati gravitazionalmente.
Abbiamo detto che gli asteroidi con diametri più piccoli di 150-200 metri sono invece considerati veri e propri blocchi monolitici, cioè frammenti collisionali, in grado di ruotare più velocemente del valore limite dato dalla spin-barrier a causa delle intense forze di coesione interne che tengono unito il corpo. Tuttavia ci sono delle eccezioni a questa “regola”, cioè esistono alcuni asteroidi con un diametro superiore ai 200 m (quindi rubble-pile secondo il modello precedente), che però hanno un periodo di rotazione al di sotto della spin-barrier.
Il primo oggetto scoperto a violare palesemente la cohesionless spin-barrier è stato l’asteroide 2001 OE84 nel 2002. Si tratta di un asteroide near-Earth che ruota in 0,4865 ore con un diametro di circa 700 metri. Altro notevole oggetto è l’asteroide main-belt (335433) 2005 UW163 che ha un periodo di rotazione di 1,290 ore e una dimensione di 600 metri, scoperto nel 2014. Uno degli ultimi asteroidi scoperti di questo tipo è il near-Earth 2011 UW158, che ha un periodo di rotazione di 0,6107 ore e una dimensione di 300×600 metri determinata tramite osservazioni radar. Ad ora però nessun asteroide con un diametro maggiore di 1 km ruota più rapidamente di 2,2 ore.
Gli asteroidi che violano la spin-barrier sono chiamati Large Super-Fast Rotator (LSFR). La loro esistenza è stata teorizzata per la prima volta da Holsapple nel 2007 e la teoria è stata successivamente arricchita e perfezionata da Sánchez e Scheeres nel 2014. Questi ultimi autori hanno esplorato la possibilità che, grazie alle forze di van der Waals che si esercitano fra i grani di regolite interstiziali, un asteroide con una struttura a rubble-pile possa avere una forza coesiva diversa da zero. In questo teoria i grani di regolite agirebbero come una specie di “colla” in grado di tenere coesi i blocchi di maggiori dimensioni.
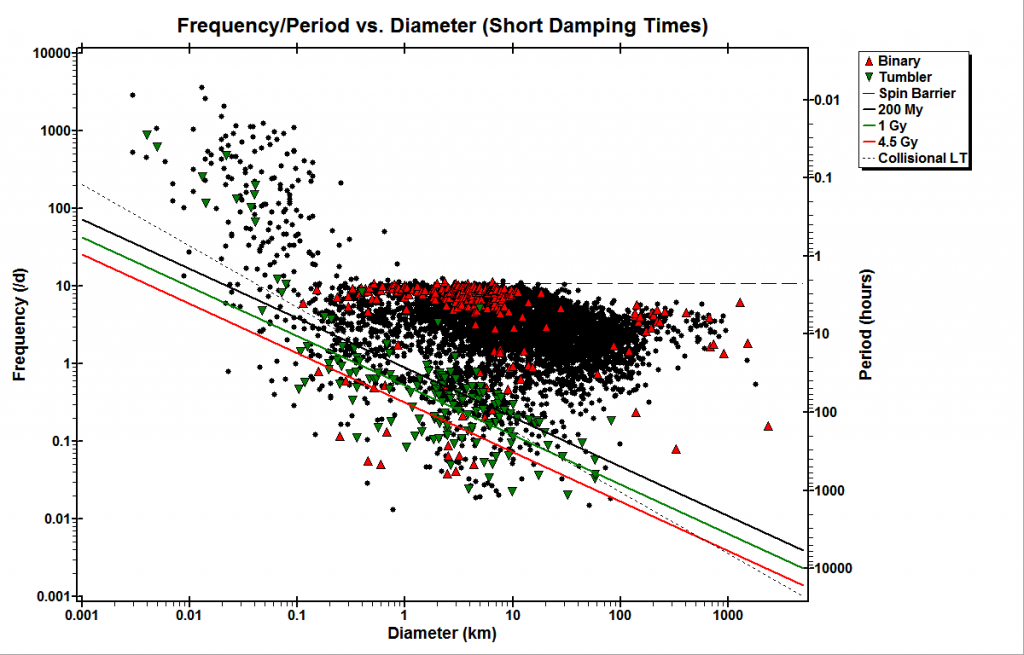
Figura 6. La frequenza di rotazione degli asteroidi (espressa in rotazioni al giorno), in funzione del diametro in km. La linea tratteggiata orizzontale è la spin-barrier, che equivale a circa 10 rotazioni/giorno. I triangoli rossi sono i sistemi binari, mentre quello verdi sono gli asteroidi con precessione dello spin (tumbler). Per spiegare l’andamento del periodo vs. diametro per gli asteroidi si ipotizza che gli oggetti più piccoli di circa 150-200 m di diametro siano blocchi monolitici, mentre i corpi più grandi sarebbero oggetti fratturati dalle collisioni composti di blocchi più piccoli, non coesi fra di loro, tenuti insieme dalla reciproca forza di gravità (struttura a “rubble-pile” senza coesione). Immagine tratta dall’Asteroid Lightcurve Photometry Database (http://alcdef.org/).
La “caccia” agli asteroidi LSFR
La forza di coesione della regolite inizia a diventare importante solo per corpi inferiori ai 10 km di diametro, quindi la ricerca di LSFR va fatta su asteroidi relativamente piccoli. Risulta chiaro che la fotometria degli asteroidi è una tecnica essenziale per andare a caccia degli asteroidi LSFR. Tuttavia l’osservazione dei piccoli MBA può essere difficoltosa. Ad esempio, se consideriamo un tipico asteroide di tipo S con 1 km di diametro posto a 2,5 UA dal Sole, all’opposizione avrà una magnitudine apparente di +20,3. Questo valore è piuttosto alto e fare la fotometria con piccoli strumenti diventa difficile. Per questo motivo è molto più facile andare alla ricerca di LSFR nella popolazione degli asteroidi near-Earth quando fanno il loro flyby con la Terra. I NEA hanno dimensioni che rientrano in quelle tipiche in cui si possono trovare i LSFR e possono diventare sufficientemente luminosi da essere osservati agevolmente anche in piccoli strumenti. L’unica “pecca” di questa strategia osservativa è che il moto proprio di un NEA può essere elevato e una sessione con le stesse stelle di confronto può diventare davvero breve se il campo di vista non è sufficientemente ampio. Per non avere troppi problemi con la durata della sessione ci si può limitare a considerare oggetti con un moto proprio non superiore ai 10 arcsec/minuto. Si tratta di osservazioni non facili ma che possono dare informazioni preziose sulla costituzione fisica dei piccoli asteroidi. Vale la pena andare a caccia di LSFR!
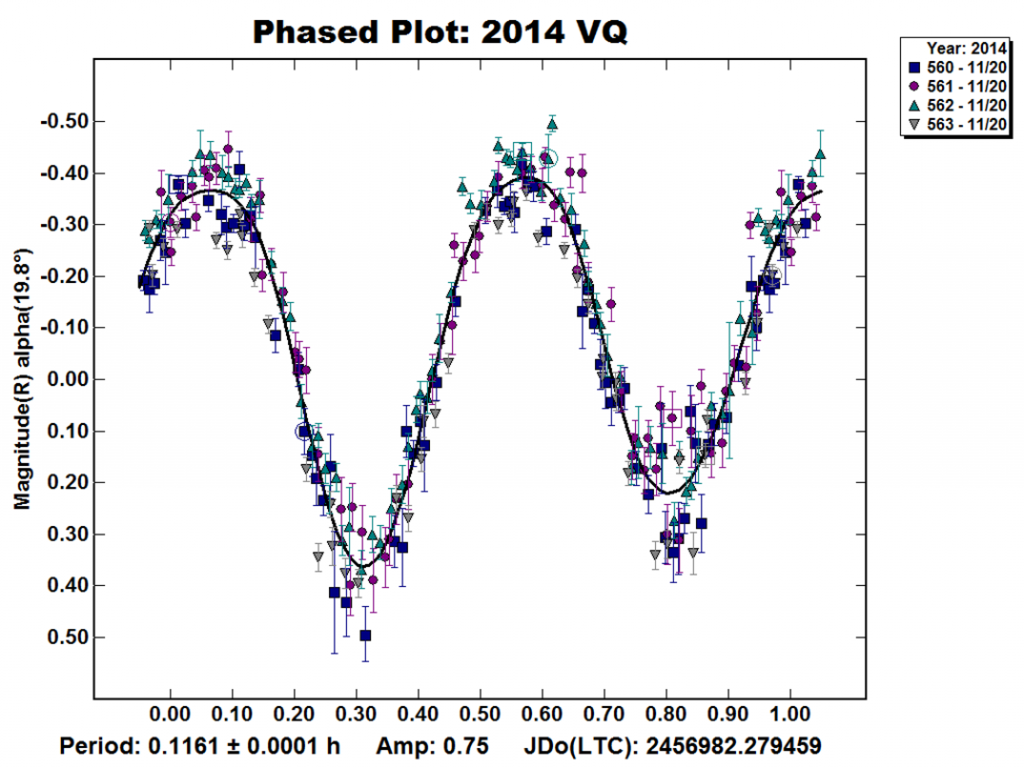
Figura 6. L’asteroide 2014 VQ è un NEA candidato ad essere un LSFR scoperto nel novembre 2014. Ha un periodo di rotazione di soli 7minuti e una dimensione che può andare da 165 metri (se di tipo V) a 267 metri (se di tipo S).
Conclusioni
Come abbiamo visto in questo breve articolo la fotometria degli asteroidi può portare a dei risultati davvero molto interessanti, sia per quanto riguarda lo studio dei singoli oggetti sia per quanto riguarda lo studio di intere popolazioni. Non abbiamo esplorato tutte le possibilità di studio ma quanto detto dovrebbe dare un’idea di quello che si può ottenere. Gli asteroidi meritano di essere studiati, come amo ripetere la migliore motivazione per fare la fotometria di un asteroide è che “non si può mai sapere quello che si troverà osservando quei piccoli punti di luce che si muovono in cielo!”.











 Figura 4
Figura 4







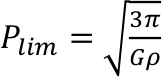 (4)
(4)



