Uno dei grandi vantaggi dei sensori digitali è la cosiddetta linearità, o risposta lineare. Di cosa si tratta? In pratica un sensore produce un’immagine la cui intensità è direttamente proporzionale alla luminosità dell’oggetto o al tempo di esposizione. Se ad esempio facciamo una foto di una stella non variabile, questo implica che se si raddoppia l’esposizione raddoppierà il segnale (la luminosità) che il sensore avrà registrato dalla stella. Detto in questi termini sembra la scoperta dell’acqua calda e si fatica persino a capirne l’utilità; anzi, gli astrofotografi più esperti neanche lo vedono come un vantaggio e vedremo presto il perché.
Che i sensori abbiano una risposta lineare all’intensità luminosa che li colpisce non è una cosa scontata. L’altro strumento che usiamo per osservare il mondo, l’occhio, NON possiede una risposta di questo tipo, ma logaritmica: in pratica l’intensità percepita da tutti gli occhi umani cresce con il logaritmo dell’intensità luminosa che lo colpisce. In questo modo, quindi, quando vediamo una sorgente che ci appare il doppio più luminosa di un’altra, la reale differenza di luminosità non è di due volte ma molto più alta. Il caso classico è rappresentato dalla scala delle magnitudini, in cui tra una stella di magnitudine 2 e una di magnitudine 4 non c’è una differenza di 2 volte come suggerisce l’occhio ma di ben oltre 6 volte. Questa curva di risposta meno ripida di una retta consente al nostro occhio di sopportare enormi differenze di luminosità senza avere particolari problemi perché di fatto schiaccia le reali differenze di luminosità e ce le fa percepire come se fossero molto più ridotte di quanto siano. Di fatto, per chi conosce un po’ il gergo della fotografia astronomica, l’occhio umano opera uno stretch logaritmico automatico su ogni immagine che registra.
Perché allora i sensori digitali possiedono una risposta lineare, così differente da quella dell’occhio umano? E perché questa sembra così importante tanto da dedicarle un post? La risposta è semplice: la linearità nella risposta è fondamentale se si vogliono effettuare precise stime di luminosità degli astri. L’introduzione dei sensori digitali nell’astronomia (professionale) ha prodotto una grande rivoluzione che ha consentito di arrivare persino a scoprire la debolissima traccia lasciata da un pianeta extrasolare in transito di fronte al disco luminoso della propria stella.
In ambito prettamente astrofotografico questo che è un enorme vantaggio viene ribaltato e si trasforma in uno svantaggio: gran parte dell’elaborazione di una foto estetica si basa infatti sui cosiddetti stretch, ovvero sull’alterare la risposta portandola da lineare a logaritmica. Questa operazione consente di osservare sullo schermo del computer sia dettagli molto deboli che molto brillanti. Se si fosse avuto un sensore già con una risposta logaritmica come il nostro occhio sarebbe stato quindi più facile ottenere fotografie estetiche, in un certo senso!
In realtà la risposta lineare del sensore serve anche per chi fa fotografia estetica e permette di correggere i principali difetti delle immagini attraverso i dark frame e i flat field. Quest’ultimi sono importantissimi nel poter disporre di un’immagine da elaborare priva di difetti macroscopici e dalla quale potremo discernere molto bene dettagli reali da artefatti dovuti a polvere sul sensore o alla vignettatura del telescopio. Se il sensore non ha risposta lineare per certi livelli di luminosità, i flat field potrebbero non correggere le immagini e il risultato potrebbe essere disastroso.
Chi si dedica alla ricerca, anche in ambito amatoriale, soprattutto fotometrica, ha l’assoluta necessità di sapere se e quanto è lineare la risposta del proprio sensore, altrimenti rischia di misurare magnitudini del tutto sballate rispetto ai dati reali. Ecco allora che ho trasformato un argomento che poco interessava in uno dei mille problemi aggiuntivi che si trovano ad affrontare tutti coloro che usano camere digitali: i sensori hanno una risposta lineare? Se sì, per tutto l’intervallo di luminosità consentito? Come possiamo capire come si comporta il nostro sensore?
Come al solito parto con le notizie brutte: non è scontato che la risposta del sensore sia lineare su tutto l’intervallo di luminosità che riesce a darci, anzi, i sensori delle reflex e in generale tutti quelli dotati di un meccanismo chiamato porta antiblooming (ABG) hanno un ristretto intervallo di linearità. Questo si traduce nell’impossibilità di fare misure fotometriche e spesso anche nella difficoltà quasi estrema di ottenere flat field che correggano bene le immagini estetiche. Quindi, se avete fatto del flat field e avete notato che “non flattano” la risposta potrebbe essere questa: non li avete fatti nell’intervallo di linearità del sensore, che potrebbe essere molto limitato.
La prossima domanda allora è scontata: come misuro l’intervallo di linearità del sensore? Come faccio a capire quando smette di comportarsi bene e inizia a fornire valori sballati di luminosità?
È qui che arriva la bella notizia, perché possiamo fare un test rapido e molto semplice, di giorno e stando comodi dentro casa. Di modi per fare questo test ce ne sono diversi, qui spiego quello più facile, rapido e chiaro. L’idea alla base è chiara: disporre di una fonte di luce fissa e fare una serie di scatti con tempo crescente, in modo da coprire tutta (o quasi) la gamma di luminosità concessa dall’elettronica del sensore. Poi misureremo la luminosità della sorgente in funzione del tempo di esposizione e costruiremo un bel grafico. Se la risposta è lineare, i punti si disporranno su una retta, altrimenti inizieranno a fare strane curve e potremo così individuare l’intervallo di luminosità in cui potremo effettuare i nostri flat field o misurare la luminosità delle stelle senza problemi.
Ora che abbiamo capito l’idea alla base, cerchiamo di metterla in pratica. Intanto la fonte di luce: ideale è una lampada a led, anche una torcia. Se abbiamo una flatbox le cose saranno ancora più semplici. Non è necessario montare la camera su un telescopio ma è sicuramente più comodo. Se non abbiamo grossi problemi, possiamo montare il telescopio in casa e metterci sopra la flat box. L’idea è quella di ottenere dei flat field con diversi tempi di esposizione, idealmente da 1 a 20-30 o più secondi, in modo che la luminosità media dell’esposizione più breve sia attorno a 1000-1500 ADU e quella dell’esposizione più lunga raggiunga la saturazione, circa a 65000 ADU se usiamo camere da 16 bit. In questi casi visualizzare l’istogramma ci sarà molto utile. Se la luminosità della flatbox è troppo forte possiamo inserire un filtro nella nostra fotocamera (tanto la linearità non dipende dalla lunghezza d’onda) o schermare la luce della flatbox con qualche foglio bianco.
A questo punto, in binning 1 (cioè a piena risoluzione) e con il sensore raffreddato (per chi se lo può permettere) effettuiamo degli scatti a esposizioni crescenti, partendo da 1 secondo fino ad arrivare alla saturazione, incrementando di un secondo ogni volta. Ripetiamo questa procedura 3 volte per avere una buona statistica (in pratica alla fine costruiremo 3 grafici indipendenti e vedremo i risultati) che ci permetterà di escludere eventuali variazioni della sorgente di luce. In alternativa possiamo mediare 5-6 singoli scatti per ogni intervallo di esposizione (ognuno dei quali calibrato con dark o con bias), come ho fatto nei risultati che troverete alla fine di questo post. Se abbiamo tempo e un CCD raffreddato, sarebbe meglio catturare circa 3-5 dark frame per ogni esposizione. Naturalmente non servono flat field perché stiamo analizzando di fatto dei flat field. Se abbiamo sensori non raffreddati non facciamo i dark ma i bias: una ventina di scatti con camera al buio e il più breve tempo di posa concesso dall’elettronica.
In fase di elaborazione non dovremo far nulla se non calibrare le nostre esposizioni. Attenzione in questo punto: i bias frame vanno bene per tutti gli scatti, mentre i dark frame sono collegati a ogni esposizione, quindi NON usiamo dark da 5 secondi per correggere le immagini da 2 secondi. So che alcuni software applicano un dark frame adattivo, ma non dobbiamo neanche pensarci!
Con le immagini calibrate adesso passiamo alla fase più noiosa: dobbiamo scegliere un’area di circa 50X50 pixel, sempre la stessa per ogni scatto e illuminata in modo circa uniforme, e annotarci il valore medio di luminosità, espresso in ADU.
In alternativa, se non ci sono forti variazioni di luminosità nell’intero campo, potremo usare tutta l’immagine come area di misurazione. Questo ci evita di dover tracciare un riquadro su ogni esposizione ma la precisione ne risentirà. Se i nostri speciali flat field possiedono variazioni di luminosità superiori al 10% nelle varie zone dell’immagine, siamo costretti a scegliere una piccola area verso il centro e con un’illuminazione più uniforme. La richiesta di luminosità uniforme lungo l’area di cui vogliamo misurare l’intensità luminosa è fondamentale per evitare che la misura venga falsata da porzioni che si trovano già oltre il range di linearità rispetto ad altre.
I programmi per fare questa misura sono quelli tipicamente astronomici, come AstroArt e MaxIm DL. Con MaxIm DL basta aprire l’immagine calibrata che si vuole misurare, visualizzare la finestra “Information Window” (View –> Information Window), e poi da questa scegliere la modalità “Area”. Di default compariranno le informazioni relative a tutta l’immagine, compresa quella che a noi maggiormente interessa: il valore medio della luminosità (Average), espresso in ADU. Se vogliamo o dobbiamo restringere l’area di misurazione, si deve tracciare un rettangolo sull’immagine con il mouse, ciccando con il tasto sinistro, tenendo premuto e trascinando il rettangolo che si formerà. In questo caso è assolutamente necessario annotarsi la posizione e le dimensioni della finestra di misurazione perché dovrà essere identica per ogni immagine che vorremo misurare, nella medesima posizione. Una volta tracciata l’area, la finestra “Information Window” ci darà le sue coordinate (quindi potremo ridisegnarla uguale senza problemi anche sulle altre esposizioni) e naturalmente i valori di luminosità media.
Area di misurazione della luminosità media con MaxIm DL e rispettiva “Information Window” in cui possiamo trovare la sua posizione e la luminosità media (Average).
Analizziamo le immagini
Bene, per ognuna delle immagini calibrate con dark frame o bias frame annotiamoci il relativo tempo di esposizione e il valore medio di luminosità. Importiamo i dati in un foglio di calcolo e cominciamo con le nostre analisi.
Come programma possiamo usare Excel o il gratuito Gnumeric, che funziona sia per Windows che per Linux. In ogni caso le operazioni da fare sono poche e semplici: si tratta infatti di costruire qualche grafico e magari fare una regressione lineare sui dati. Niente paura, spiego tutto nei prossimi punti.
- Il primo grafico che dobbiamo fare mette in correlazione il tempo di esposizione e il valore medio di ADU misurato per ogni immagine. Sull’asse x va quindi il tempo di esposizione dei nostri speciali flat field, sull’asse y i valori medi di ADU. Da questo grafico, se abbiamo fatto tutte le misure per bene, dovremo trovare dei punti che si dispongono su una retta perfetta: caspita, il sensore è perfettamente lineare allora! No, non necessariamente. Questo è il primo grafico e serve per vedere se ci sono stati errori macroscopici nella fase di acquisizione ed estrapolazione dei dati (o se il sensore fa proprio schifo!). Con il grande intervallo di luminosità sull’asse y è impossibile vedere piccole deviazioni dal comportamento lineare. Quando la situazione può ingannare l’occhio (cioè quasi sempre), ecco che subentra una cosa che gli uomini hanno inventato tanto tempo fa e che i più, ahimé, disprezzano: si chiama scienza, in questo caso un po’ di statistica. La domanda a cui vogliamo rispondere è la seguente: il grafico ci sembra perfetto perché è così o perché siano stati ingannati? La risposta l’ho già data implicitamente qualche riga sopra, meglio quindi procedere spediti per vedere che avevo ragione;
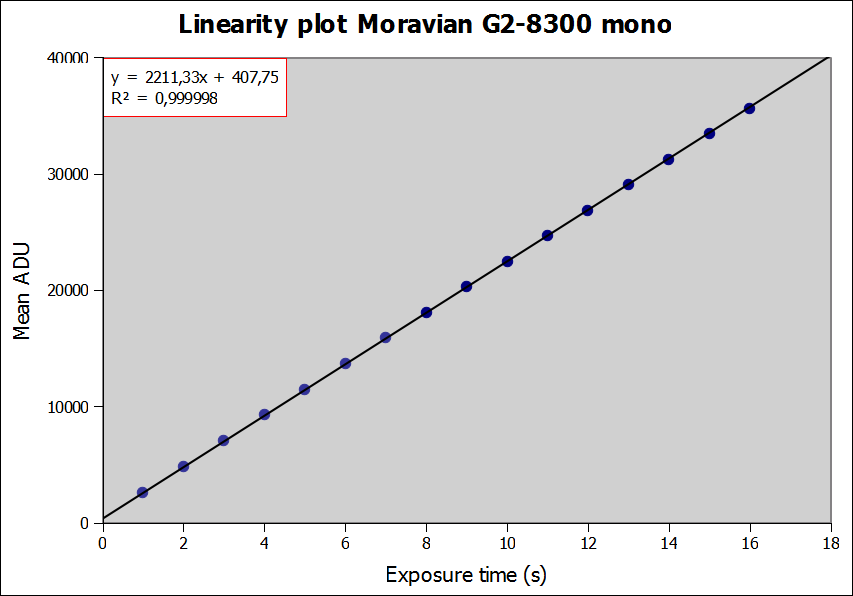
Di primo acchitto il grafico sembra molto bello, ma l’occhio inganna…
- A dominare il grafico non sono le probabili piccole deviazioni dal comportamento lineare ma il fatto che la luminosità cambia di migliaia di ADU lungo l’asse Y. Per togliere questo comportamento e mettere a nudo le più piccole imperfezioni del nostro sensore, dobbiamo fare quella che viene chiamata regressione lineare o fit lineare e analizzare i residui. In pratica diciamo al software di “unire” i punti con la migliore retta che è possibile costruire, poi sottrarremo i valori della retta ai punti reali e analizzeremo quelli che vengono chiamati residui, ovvero i punti depurati dell’andamento principale che ci impediva di vedere nel dettaglio il loro comportamento. Se i punti sono davvero tutti sulla retta come sembra dal primo grafico, i loro residui saranno tutti nulli o disposti in modo casuale attorno allo zero, e noi saremo contentissimi perché avremo in tasca il sensore digitale più preciso dell’Universo intero. Tranquilli, non c’è pericolo di cadere in questa eventualità…
Sembra tutto complicato ma non lo è. Ci sono diversi modi per fare un fit lineare e poi sottrarne i valori ai dati. Con il programma Gnumeric, ad esempio, un modo molto rapido e user friendly è farlo fare in modo grafico al programma. Nelle opzioni di costruzione del grafico (che si attivano quando vogliamo costruire un nuovo grafico o quando facciamo doppio click su uno già creato), se ci posizioniamo sulla serie di dati immessi e clicchiamo sul punsalte “Aggiungi” potremo scegliere una bella “Trend line to serie 1”, in particolare del tipo “Lineare”. Nel nuovo menù che si apre basta accertarsi che l’opzione “Affine” sia selezionata e già potremo vedere una bella retta sovrapposta ai nostri dati.
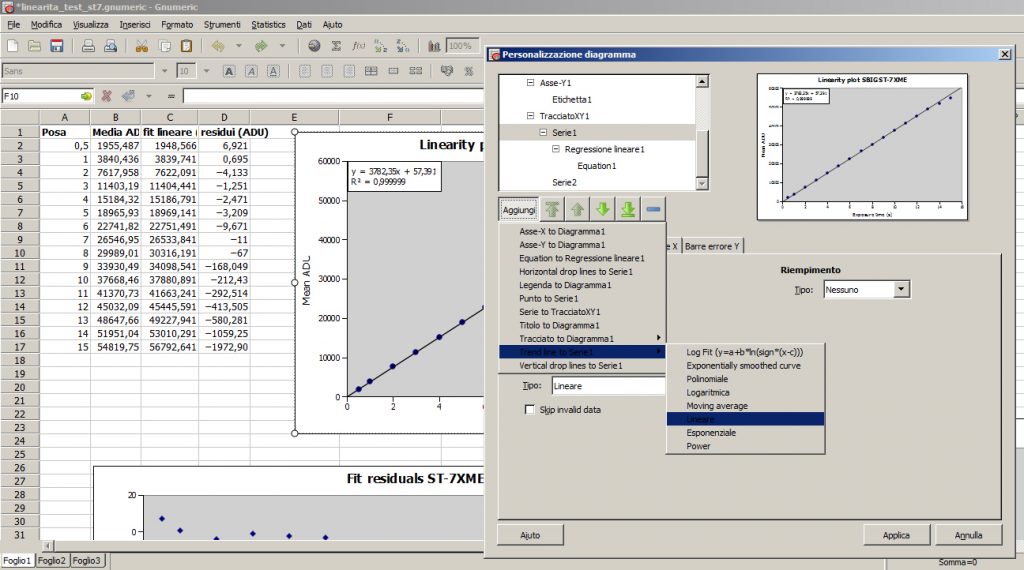
In gnumeric, in pratica un clone gratis di Excel, possiamo fare tutti i calcoli che vogliamo. In questo caso ci serve un fit lineare e poi magari di visualizzare l’equazione della retta.
- Non abbiamo ancora finito, però. Clicchiamo ancora su “Aggiungi” e selezioniamo “Equazione to Regressione lineare 1”. Confermiamo tutto e vedremo comparire nel grafico sia la retta di fitting che l’equazione che la descrive. A questo punto dobbiamo creare una nuova colonna nel nostro foglio di lavoro, alla quale applichiamo l’equazione a ogni tempo di esposizione. In questo modo invece di una retta troveremo dei punti che si sovrappongono a essa in modo perfetto. Non c’è bisogno di graficarli; questi ci servono per fare la successiva operazione: creare i residui. I punti appena ottenuti sono quelli che si avrebbero in una situazione ideale in cui la risposta è rappresentata da un’unica e perfetta retta. I nostri punti sperimentali, invece, non avranno questa bella proprietà. Per capire quanto se ne discostano basta creare una nuova colonna in cui calcoliamo la differenza Osservato – Calcolato per ogni tempo di esposizione.

- Proviamo ora a costruire un grafico di questi residui in funzione del tempo di esposizione o, meglio, del valore medio di ADU corrispondente e vedremo che quella che prima era una retta perfetta ora in realtà è molto diversa.
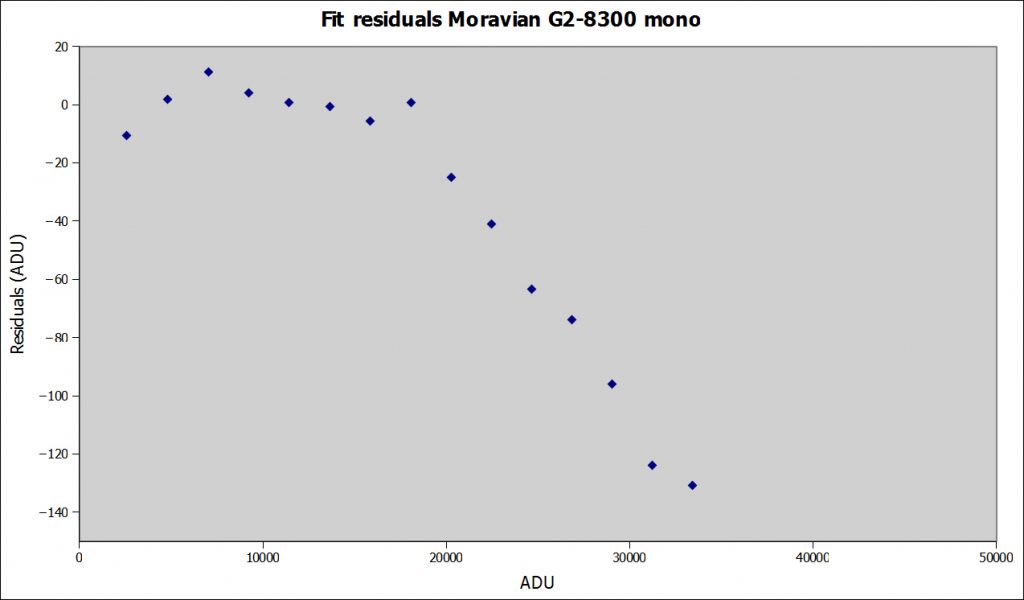
Ora le cose sono più chiare e i dati non sono poi così ben disposti su una retta, che in questo caso dovrebbe essere parallela all’asse x!
Questo è il grafico davvero importante, perché ci dice come cambia il comportamento del nostro sensore in funzione della luminosità. Nella migliore delle ipotesi vedremo un intervallo lungo fino ad almeno 30 mila ADU in cui i punti si trovano su una retta quasi perfetta e poi divergono. Questo è il caso classico delle camere CCD scientifiche, tipicamente monocromatiche e prive della porta antiblooming.
Nella peggiore delle ipotesi, ovvero nel caso di camere CCD o reflex dedicate all’imaging estetico, le cose saranno ben peggiori, con diversi andamenti di “linearità” prima della saturazione. In questi casi diventa impossibile fare fotometria di alta precisione e spesso è complicato anche fare corretti flat field per riprese con soggetti deboli.
Due esempi reali
Ho effettuato il test di linearità appena esposto per due sensori CCD. Il primo, un Kak-402 con microlenti che equipaggia una SBIG ST-7XME, è il tipico sensore scientifico: monocromatico e senza antiblooming. Il secondo, un Kaf-8300 che equipaggia molte camere CCD, in questo caso una Moravian G2-8300 monocromatica, dotato di porta antiblooming, quindi più adatto all’imaging estetico.
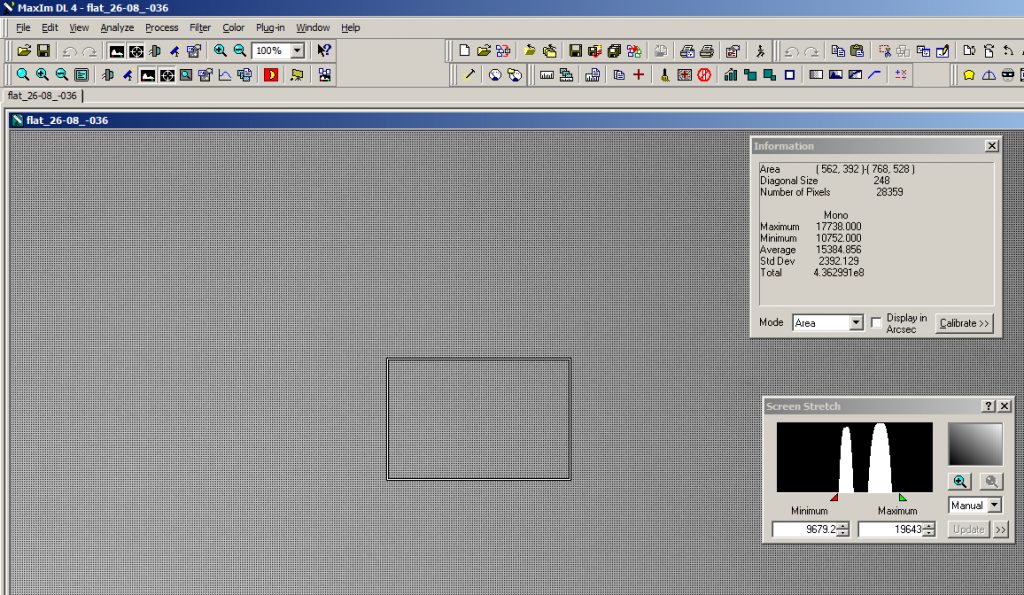
I risultati evidenziano molte differenze. Se a prima vista i grafici della luminosità media in funzione del tempo di esposizione sono identici, o addirittura sembrano migliori nella Moravian (ma solo perché non si è raggiunta la saturazione, cosa che è avvenuta con la SBIG):
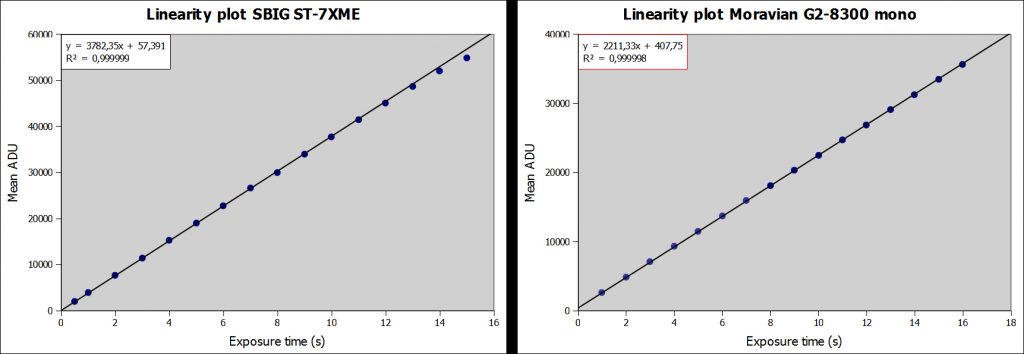
Test di linearità per due sensori CCD. Questi i grafici degli ADU medi in funzione del tempo di esposizione. Ci dicono poco e potrebbero ingannare.
Il fitting lineare con conseguente analisi dei residui rivela la reale situazione:

Analisi dei residui: ora è fin troppo evidente quale sia il sensore migliore quanto a risposta lineare. Il Kaf 8300 presenta delle vere e proprie montagne russe!
Come si può vedere, la SBIG, a partire da circa 2000 ADU e fino a 25000 presenta una linearità che sfiora la perfezione, con un comportamento da manuale. Gli scostamenti dalla retta ideale sono dell’ordine dello 0,01%, ovvero di una parte su 10 mila. Questo consente ad esempio di mettere in evidenza senza problemi differenze di magnitudine dell’ordine del millesimo e rivelare quindi anche pianeti extrasolari in transito. Oltre i 30 mila ADU il comportamento comincia lentamente a divergere dalla linearità, sebbene bisogna superare i 40 mila per avere una non linearità dell’ordine dell’1%.
D’altra parte il grafico dei residui del Kaf-8300 è molto meno regolare. Si possono vedere almeno tre zone indipendenti, ognuna approssimabile con una retta di diverso coefficiente angolare: la prima fino a 9 mila ADU, la seconda da 10 mila a circa 18 mila e la terza da 20 mila a 30 mila, prima della naturale deviazione asintotica verso i valori di saturazione. Questo è un problema se si vuole fare fotometria di alta precisione, in pratica impossibile, ma anche per i flat field. Quale valore usare per fare corretti flat field? La risposta forse già l’abbiamo vista da qualche altra parte, ma ora ne abbiamo la prova: per correggere un fondo cielo che tipicamente ha valori di poche migliaia di ADU, occorre che il flat field sia fatto nel primo intervallo di linearità, ovvero quello fino a 9000 ADU. In pratica, un buon flat field per un sensore di questo tipo è la media di tanti singoli flat che hanno come luminosità di picco circa 8000, massimo 9000 ADU. Per la ST-7XME invece, e in generale per tutte le camere sprovviste di porta antiblooming, i flat field si possono fare attorno a 25 mila ADU, in modo da avere il maggior rapporto segnale/rumore pur rimanendo ancora entro la zona perfettamente lineare.
Il test può essere fatto anche con le reflex senza problemi: basta scattare in formato raw agli ISO che di solito si usano per fare riprese astronomiche. In questo caso sarebbe interessante capire se e quanto varia la linearità della risposta in funzione degli ISO e in generale come si comportano questi sensori. Basta provare!